Question

Paul has $40000 to invest. His intent is to earn 9% interest on his investment. He can invest part of his money at 6% and part at 10% interest. How much does paul need to invest in each option to make a total of 9% return on his $40000 ?

Answer 1

Given

Paul has $40000 to invest &he can invest part of his money at 6% and part at 10% interest.

Find out Paul invest in each option to make a total of 9% return on $40000 .

To proof

Paul invest = $ 40000

let us assume that x be the part of money he invested at 6%.

let us assume that (40000 - x) be the part of money he invested at 10 %.

6% written in the simpler form

`= (6)/(100)`

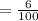
= 0.06

similarly,

10% written in the simpler form = 0 .1

9% written in the simpler form = 0.09

than the equation becomes

0.09 (40000) = (40000 - x ) 0.1 + 0.06x

3600 = 4000 - 0.1x + 0.06x

0.1x - 0.06x = 4000 - 3600

0.04x = 400

x = 10000

$ 10000 be the part of money he invested at 6%.

$30000 be the part of money he invested at 10 %.

Hence proved

Answer 2

Paul needs to invest $10000 at 6% interest and $30000 at 10% interest to make a total of 9% return on his $40000.

Step-by-step explanation

Suppose, the amount of money at 6% interest is
`x`

As Paul has total $40000 to invest, so the amount of money at 10% interest will be:
`(40000-x) dollar`

His intent is to earn 9% interest on his $40000 investment. So, the equation will be......

`0.06x+0.10(40000-x)=0.09*40000\\ \\ 0.06x+4000-0.10x=3600\\ \\ -0.04x=3600-4000=-400\\ \\ x=(-400)/(-0.04)=10000`

So, Paul needs to invest $10000 at 6% interest and ($40000- $10000) or $30000 at 10% interest to make a total of 9% return on his $40000.