Question

In a right triangle abc, cd is an altitude, such that ad=bc. Find ac, if ab=3 cm, and cd= square root 2 cm.

Answer 1

ΔACB ΔCDA

AC² + BC² = AB² AD² + CD² = AC²

BC² = AB² - AC² BC² + CD² = AC² (AD=BC is given)

BC² = AC² - CD²

AB² - AC² = AC² - CD² (both sides were = to BC²)

AB² + CD² = 2AC²

(3)² + (√2)² = 2AC² (AB=3 and CD=√2 were given)

9 + 2 = 2AC²

11 = 2AC²

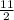`(11)/(2)` = AC²

`\sqrt{(11)/(2) }` = AC

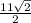`(11√(2) )/(2)` = AC