Question

Chay throws an object straight up into the air with an initial velocity of 60 ft/s from a platform that is 40 ft above the ground. Use the formula h(t)=−16t2+v0t+h0 , where v0 is the initial velocity and h0 is the initial height. How long will it take the object to hit the ground? Round your answer to the nearest tenth of a second.

Answer 1

Explanation:

Answer 2

The object will hit the ground in 4.3 s.

The formula used for the object thrown by Chay is:

`h(t)=-16t^(2)+v_(0)t+h_(0)`

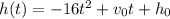
According to the problem,

Initial velocity
`v_(0)=60ft/s`

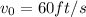
Initial height
`h_(0)=40ft`

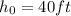
Therefore,

`h(t)=-16t^(2)+60t+40`

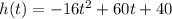
When the object hits the ground h(t) becomes 0.

Thus,

`0=-16t^(2)+60t+40`

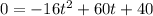
Dividing both sides by 4 we get;

`4t^(2)-15t-10=0`

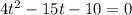
Solving by applying quadratic formula;

`x=\frac{-b+/-\sqrt{b^(2-4ac) } }{2a}`

`t=\frac{15+/-\sqrt{15^(2)+160 } }{8}`

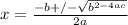
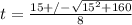
t=4.3s