Answer:
 for all values.
for all values.
Explanation:
Given :
 and
and
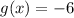
To find : The description of
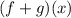
Solution :
We have given,
 and
and
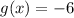
Using property,
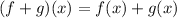
Substituting the values,
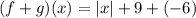
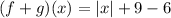
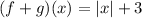
If we put any value of x in to this function,
We get a value that is greater than or equal to 3.
Refer the attached figure below.