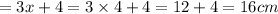Question

Point P is the midpoint of both MR and NQ, which are on the same line. If MN=26, NP=3x+4, and QR=6x+2, find NP.

Answer 1

Answer: NP= 16 cm

Explanation:

As we shown in the figure below :

Since P is the midpoint of MN and NQ

So, We consider ΔMNP and ΔPQR,

∠MPN=∠QPR (∵ Vertically opposite angles are equal)

MP=PR (∵ P is the mid point of MR)

NP=PQ (∵P is the midpoint of NQ)

So, ΔMNQ ≅ ΔPQR (∵By SAS congruence )

∴
`26=6x+2 \text{(By CPCT )}\\26-2=6x\\24=6x\\(24)/(6)=x\\4=x`

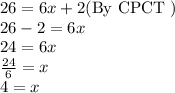
So, NP
`=3x+4=3* 4+4=12+4=16 cm`