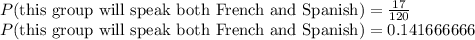Question

A group of 120 people touring Europe includes 45 people who speak French, 42 who speak Spanish, and 50 who speak neither language. What is the probability that a randomly chosen tourist from this group will speak both French and Spanish?

Answer 1

Answer :
`P(\text{this group will speak both French and Spanish})=0.141666666`

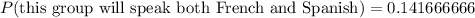
Step-by-step explanation:

Since we have given that

n(U) = 120, where U denotes universal set ,

n(F) = 45, where F denotes who speak French,

n(S) = 42 , where S denotes who speak Spanish,

n(F∪S)' = 50

n(F∪S) = n(U)-n(F∪S) = 120-50 = 70

Now, we know the formula, i.e.

n(F∪s) = n(F)+n(S)-n(F∩S)

⇒ 70 = 45+42-n(F∩S)

⇒ 70 = 87- n(F∩S)

⇒ 70-87 = -n(F∩S)

⇒ -17 = -n( F∩S)

⇒ 17 = n(F∩S)

`P(\text{this group will speak both French and Spanish})= (17)/(120)\\P(\text{this group will speak both French and Spanish})=0.141666666`