The distance between two points can be found by looking at the distance as the hypotenuse of a right triangle, where the bases are the distance between the x values (movement from left to right) and the y values (movement up or down). The formula looks like this:
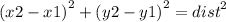
So,
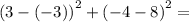
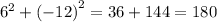
and
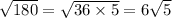
so the distance is
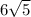
to find the missing y, we use the midpoint formula: (x,y) where
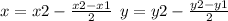
we just need the y, so
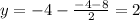
so y=2
now, the next question, we use the midpoint formula to find the midpoint between (7,8) and (-3,2)
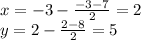
so our midpoint is at (2,5)
The next question is a bit more complicated. We use the distance formula and substitute in every point until we get an answer of 5.
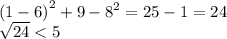
so it is not A.
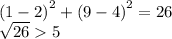
so it is not B
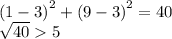
so it is not C
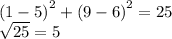
so the answer is D (5,6)
Finally, some algebra and the midpoint formula can give us y.
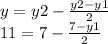
multiply everything by 2 to get rid of the denominator then combine like terms.
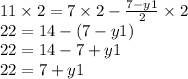
finally, the 7 is positive, so we need to subtract 7 from both sides.
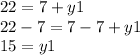
so our missing y is 15.
hope that helps!