We have to determine the value of

= (5(9)+6) + (5(10)+6) +(5(11)+6) + .......... + (5(21)+6)
= 51+56+61+66+ ........ + 111
Since, the common difference is 5, hence this series is in arithmetic progression.
Sum of AP is given by the formula:
![(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/it2selg8vh4bx16zfe6wb5k4c8bqp7f8fa.png)
Since, there are 13 terms.
=
![(13)/(2)[2(51)+(13-1)5]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/w58ybes5ql9cjfvmg2j9ywd6tgit3b0hir.png)
=
![(13)/(2)[102+60]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/k4qxxgc4cpoa0k49b08tx81l7mqwkwq9gx.png)
=
![(13)/(2)[162]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/s2a8uj5glswizra07bhmkawv51w5w1n9qt.png)
=
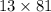
= 1053
Therefore, the sum of the series is 1053.
So, Option G is the correct answer.