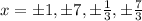Question

The polynomial function f(x) = 3x5 – 2x2 + 7x models the motion of a roller coaster. The roots of the function represent when the roller coaster is at ground level. Which answer choice represents all potential values of when the roller coaster is at ground level? Begin by factoring x to create a constant term.

Answer 1

At x=0 the roller coaster is at ground level. All the potential roots are

`x=0,\pm 1, \pm 7, \pm (1)/(3), \pm (7)/(3)`.

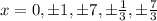Explanation:

The given function is

`f(x)=3x^5-2x^2+7x`

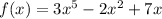
It is given that the roots of the function represent when the roller coaster is at ground level.

The factor form of given function is

`f(x)=x(3x^4-2x+7)`

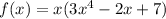
To find the roots of the function equate f(x)=0.

`0=x(3x^4-2x+7)`

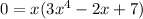
By using zero product property, equate each factor equal to 0.

`x=0`

`3x^4-2x+7=0` ...(1)

The equation (1) has no real root.

To find the potential root use rational root theorem.]

According to the rational root theorem, all the possible roots are in the form of

`r=\pm \frac{\text{Factors of constant term}}{\text{Factors of leading term}}`

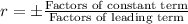
The leading term is 3 and the constant term is 7.

Factors of 7 are ±1, ±7 and the factors of 3 are ±1 and ±3.

All the possible roots are

`x=\pm 1, \pm 7, \pm (1)/(3), \pm (7)/(3)`