Answer:
A.
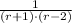
Explanation:
We have been given an expression
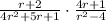 . We are asked to simplify our given expression.
. We are asked to simplify our given expression.
We will factor the denominators of both fractions as shown below:
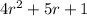
 Splitting the middle term.
Splitting the middle term.
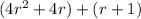 Making groups.
Making groups.
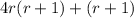 Factor out 4r from 1st group.
Factor out 4r from 1st group.
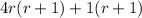 Factor out 1 from 2nd group.
Factor out 1 from 2nd group.
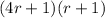
Using difference of squares we will factor the 2nd denominator as:
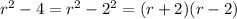
Substituting these values in our given problem we will get,
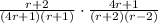
After cancelling out terms we will get,
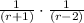
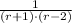
Therefore, option A is the correct choice.