Question

Please check my homework on Negative Indices!

Just need confirmation that I'm doing the right thing here.


`(2p^(-3) q^(8) )^(4)`
I got
`(16q^(32) )/(p^(12) )`


`(2m^(-4)n^(5))^(-2)`
I got
`(m^(8) )/(4n^(10) )`


`2(5g^(-4)h^(-6))^(2)`
I got
`(2)/(25) g^(8)h^(12)`


`4(2c^(-3)d^(6))^(-5)`
I got
`(c^(15) )/(8d^(30) )`

Answer 1

Our first expression is
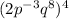`(2p^(-3) q^(8) )^(4)`. Upon distributing the exponent 4 on all the terms, we get:

`(2p^(-3) q^(8) )^(4)=2^(4)(p^(-3))^(4)(q^(8))^(4)=16p^(-12)q^(32)=(16q^(32))/(p^(12))`

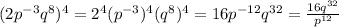
Therefore, your answer is correct for this part. :)

Second expression is
`(2m^(-4)n^(5))^(-2)`. Upon distributing the exponent -2 on all the terms, we get:

`(2m^(-4)n^(5))^(-2)=2^(-2)(m^(-4))^(-2)(n^(5))^(-2)=2^(-2)m^(8)n^(-10)=(m^(8))/(4n^(10))`

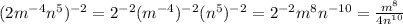
Your second answer is correct too.

Our third expression is
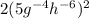`2(5g^(-4)h^(-6))^(2)`. Upon distributing the exponent 2 on all the terms, we get:

`2(5g^(-4)h^(-6))^(2)=2(5^(2))(g^(-4))^(2)(h^(-6))^(2)=2(25)g^(-8)h^(-12)=(50)/(g^(8)h^(12))`

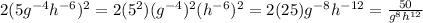
This one is not correct. Your answer would have been correct, if the exponent were -2 instead of 2 in this part.

Our forth and last expression is
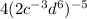`4(2c^(-3)d^(6))^(-5)`. Upon distributing the exponent -5 on all the terms inside the parenthesis, we get:

`4(2c^(-3)d^(6))^(-5)=4(2^(-5))(c^(-3))^(-5)(d^(6))^(-5)=(4)/(2^(5))(c^(15))(d^(-30))=(4c^(15))/(32d^(30))=(c^(15))/(8d^(30))`

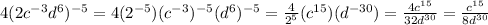
Therefore, your answer for this part is also correct.

Looking at your work, I don't think you made a mistake in number 3 also, probably mis-typed the question while writing here :)