Let us consider two velocity vectors A and B.
Assume that magnitude of A is greater than equal to magnitude of B i.e
n[A] ≥ n[B] [Here n[X] represents the magnitude of vector X]
As per the questions the vectors are opposite in direction.
Now we have to calculate the resultant of these two vectors.
As per parallelogram law of vector addition,the resultant of two vectors will be-
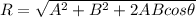
As per the given question
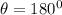 [vectors are opposite in direction]
[vectors are opposite in direction]
Hence the resultant
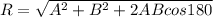
![R=\sqrt{A^(2)+B^(2)+2AB[-1] }](https://img.qammunity.org/2019/formulas/physics/high-school/ricso4l0t2coprgeqvizj58ontd6rlp0yn.png) [cos180= -1]
[cos180= -1]
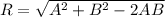

The direction of resultant will be always along the bigger vector.Hence it is along the direction of vector A.
we know that n[A] ≥ n[B] also n[A-B]≤ n[A] .
⇒n [R] ≤ n[A].
Hence the resultant of the velocities will be smaller in magnitude as part of vector B will cancel vector A.
Hence third option is right.