Question

PQ has endpoints P(5,-3) and Q(2,4). whats the midpoint? whats the quadrant?

Answer 1

Midpoint has x=(5+2)/2= 7/2=3.5 and y= (-3+4)/2=1/2= 0.5

Midpoint is ( 3.5 , 0.5 )

the quadrant is (7/4, 1/4)

Answer 2

Answer: The required midpoint is (3.5, 0.5) and it lies in Quadrant 1.

Step-by-step explanation: Given that a line segment PQ has endpoints P(5, -3) and Q(2, 4).

We are to find the midpoint of PQ and the quadrant in which it lies.

We know that

the co-ordinates of the midpoint of a line segment with endpoints (a, b) and (c, d) are given by

`\left((a+c)/(2),(b+d)/(2)\right).`

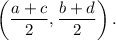
Therefore, the required co-ordinates of the midpoint of PQ is given by

`\left((5+2)/(2),(-3+4)/(2)\right)\\\\\\=\left((7)/(2),(1)/(2)\right)\\\\=(3.5,0.5).`

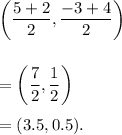
Since both the co-ordinates are positive, so the midpoint lies in Quadrant 1.

Thus, the required midpoint is (3.5, 0.5) and it lies in Quadrant 1.