Question

Find the values of m for which the lines y=mx-2 are tangents to the curve with equation y=x^2-4x+2

Answer 1

Let y= mx-2 be the tangent line to y=x^2-4x+2 at x=a.

Then slope,
`m=(dy)/(dx) at x=a = 2a-4.`

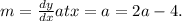
Hence the equation is y=(2a-4)x-2

Let's find y-coordinate at x=a using tangent line and curve.

Using tangent line y at x=a is (2a-4) a -2
`=2a^(2)-4a-2`

Using given curve y-coordinate at x=a is
`a^(2)-4a+2`

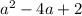
Let's equate these 2 y-coordinates,

`2a^(2) -4a-2 = a^(2) -4a+2`

`2a^(2)-a^(2) = 2+2`

`a^(2)=4`

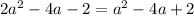
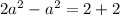
a=2 or -2.

If a=2,
`m=2a-4 = 2*2-4=0`

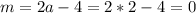
If a=-2,
`m= 2(-2)-4 = -8`

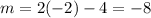
Hence m values are 0 and -8.