Question

For what value(s) of x does y = 0 for the function tan(x)?

-270°, -90°, 90°, and 270°

-270°, -90°, 0°, 90°, and 270°

-360°, -180°, 0°, 180°, and 360°

-360°, 0° and 360°

Answer 1

So We Know That tan(x) Equals


`\tan(x) = ( \sin(x) )/( \cos(x) )`
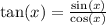
We Can Use Logic, We Know That Anything That Makes The Denominator 0, Will Not Work, So We Need To Know What Makes Sin(x) equal to 0 and Cos(x) equal to 1 or -1 BUT NOT 0


`\sin(0) = 0 \: \cos(0) = 1 \\ \sin(180) = 0 \: \cos(180) = - 1 \\ \sin(360) = 0 \: \cos(360) = 1 \\ \sin( - 180) = 0 \: \cos( - 180) = - 1 \\ \sin( - 360) = 0 \: \cos( - 360) = 1`

`\cos(90) = 0 \\ \cos( - 90) = 0 \\ \cos(270) = 0 \\ \cos( - 270) = 0`
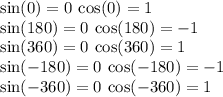
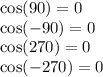
We Didn't Want Cosine To equal Zero Because Then We Get


`\tan(x) = ( \sin(x) )/( \cos(x) ) \\ \tan(x) = ( \sin(90) )/( \cos(90) ) \\ \tan(x) = (1)/(0) \\ \tan(x) = indeterminate`

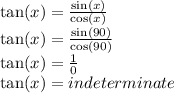
THE ANSWER IS C : -360°,-180°,0°,180°,360°