Answer:
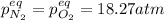
Step-by-step explanation:
Hello,
In this case, for the given chemical reaction, the law of mass action turns out:
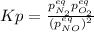
Whereas the equilibrium pressures, based on the stoichiometry and the change
 , changes to:
, changes to:
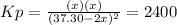
Solving for
 via quadratic equation, one obtains:
via quadratic equation, one obtains:
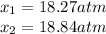
In such a way, the feasible solution is 18.27 atm since the other pressure lead to a negative pressure of NO at the equilibrium, therefore, the equilibrium pressures of nitrogen and oxygen that are equal, result in:
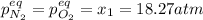
Best regards.