Question

Help me i cannot answer this guestion

Answer 1

We are given fuctions h:x --> px+6 and

inverse function h^-1 : x= 2/3 x +q.

Let us write given function in the form of y first.

h:x --> px+6 can be written as

y= px+6.

Let us find it's inverse now.

In order to find the inverse of a function, we need to switch x's and y's and then solve for x.

So, first switching x and y in y= px+6.

We get

x=py+6.

Subtracting 6 from both sides, we get

x-6=py+6-6.

x-6 = py.

Dividing both sides by p, we get

`((x-6))/(p)=y`

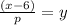
Therefore, inverse function is

`y=((x-6))/(p)`

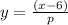
Or
`h^(-1)=((x-6))/(p)`

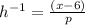
We are given inverse function

`h^(-1) =(2)/(3)x+q`

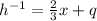
Equating both inervse functions, we get

`(2)/(3)x+q=((x-6))/(p)`

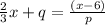
Let us write left side as a common denominator and splitting right side into two fractions, we get

`(2)/(3)x+(3q)/(3) =((x))/(p)-(6)/(p)`

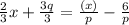
Or

`(2)/(3)x+(3q)/(3) =(1)/(p)x-(6)/(p)`

On comparing left side and right side, we get

`(2)/(3)=(1)/(p) \ and \ \ \ (3q)/(3)=(6)/(p)`

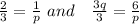
On corss multipication
`(2)/(3)=(1)/(p)` ,we get

2p = 3.

Dividing both sides by 2, we get

p =3/2.

Let us solve
`-(3q)/(3)=(6)/(p)` now.

On cross multiplication, we get

-3pq = 18

Plugging value of p, we get

-3(3/2)q = 18

-9/2 q = 18.

Multiplying both sides by 2, we get

-9q =36.

Dividing both sides by 9, we get

-q=4.

Therefore, values p=3/2 and q = -4.