Question

Emilia saved nickels, dimes, and quarters in a jar. She had as many quarters as dimes, but twice as many nickels as dimes. If the jar had 844 coins, how much money had she saved?

Answer 1

Hence, the amount of money he has saved is:

$ 94.95

Explanation:

It is given that:

Emilia saved nickels, dimes, and quarters in a jar.

Also,

She had as many quarters as dimes, but twice as many nickels as dimes.

This means that:

If the number of quarters in jar= x

The number of dimes in jar= x

and hence number of nickels in the jar= 2x

Also, the total number of coins in the jar= 844

i.e.

x+x+2x=844

i.e.

4x=844

i.e.

x=844/4

i.e.

x=211

• Hence, number of quarters in jar= 211

• The number of dimes in jar= 211

• and hence number of nickels in the jar= 2×211=422

• We know that:

1 quarter= 0.25 dollar

Hence,

211 quarter= 211×0.25=$ 52.75

• Also,

1 dime= $ 0.10

Hence,

211 dime= $ (0.10×211)=$ 21.1

• and

1 nickel=$ 0.05

Hence,

422 nickel= $ (422×0.05)=$ 21.1

Hence, the total amount of money in the jar is:

Total amount= $ 52.75+ $ 21.1+ $ 21.1

i.e.

Total amount= $ 94.95

Answer 2

Let us assume number of nickels = n,

number of dimes = d and

number of quarters = q.

Total number of coins = 844.

We can setup a statement "number of nickels + number of dimes +number of quarters = Total coins.

And we can setup an equation for the above statement as

n+d+q = 844 ---------------------equation(1).

We also given: Emilia had as many quarters as dimes.

Therefore, number of quarters = number of dimes.

So, we can setup another equation as

q = d ------------------------equation(2).

Also given : "twice as many nickels as dimes".

We can setup another equation for this statement as

n = twice of number of dimes

or n= 2d -------------------------- equation (3).

We got three equations.

Let us solve system of three equation by substitution method.

Substituting q = d and n= 2d in equation (1), we got

n+d+q = 844 => 2d +d + d = 844.

Adding d's, we get

4d =844.

Dividing both sides by 4, we get

`(4d)/(4)=(844)/(4)`

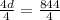
d = 211.

Therefore number of dimes = 211.

Let us find number of nickels and number of quarter coins now.

We know, number of quarters = number of dimes.

Therefore, number of qurters = 221.

Total number of coins = 844.

Therefore, number of nickels = 844 - (number of quarters + number of dimes).

= 844 -(221+221) = 844 - 442

= 402.

So, the number of nickels =402.

Let us find the total values of all the coins.

A nickel = $0.05

A dime = $0.10

A quarter = $0.25.

Total value = 0.05 *(number of nickels) + 0.10*(number of dimes) + 0.25*(number of quarters).

= 0.05* 402 + 0.10 *221 + 0.25*221.

= 20.10 + 22.10 + 55.25.

= 97.45.

Therefore, total value of all 844 coins = $97.45.

Emilia had saved $97.45.