Let us start with the explanation:
A rule of polygons says that the sum of the exterior angles always equals 360 degrees.
First of all we need to know the Interior and Exterior angle formulas:
It says the sum of the measures of the interior angles of a polygon with
 sides is
sides is
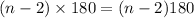 .
.
Now If we count one exterior angle at each vertex, the sum of the measures of the exterior angles of a polygon is always 360°.
Let's talk about Hexagon first : It has got 6 sides so,
 .
.
Since the skater is going around the hexagon, we need to find the sum of the measure of exterior angles ,
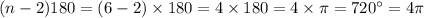
Talking about Octagon, it has got 8 sides so,
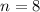 . So the sum of the measure of exterior angles is:
. So the sum of the measure of exterior angles is:
Plugging the value of 'n' we get:

Now, finding the sum of measure of exterior angles for a
 sided polygon. We get:
sided polygon. We get:

Therefore, when the skater goes around a hexagon he covers
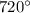 , when he goes around an octagon he covers
, when he goes around an octagon he covers
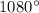 , and when he goes around a regular
, and when he goes around a regular
 sided polygon , he covers
sided polygon , he covers
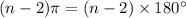 .
.