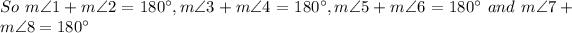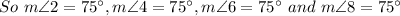Question

The sum of measures of two alternate interior angles of two parallel lines with a transversal is 210°. What are the possible measures of the angles formed by the parallel lines and the transversal?

Answer 1

105 degrees

Explanation:

Answer 2

If the lines are parallel, then the alternate interior angles are congruent.

As the sum of measures of the two alternate interior angles = 210°

⇒ Measure of one alternate interior angles = 105°

`So \ m\angle 1 = m\angle3=105^(\circ)= m\angle5= m\angle 7`

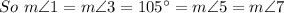
Since a straight angle contains 180º, the two angles forming a linear pair also contain 180º when their measures are added (making them supplementary).

`So \ m\angle 1 + m\angle2 = 180^(\circ),m\angle 3 + m\angle4 = 180^(\circ),m\angle 5+ m\angle6 = 180^(\circ) \ and \ m\angle 7 + m\angle8 = 180^(\circ)`

`So \ m\angle 2= 75^(\circ), m\angle4=75^(\circ), m\angle 6=75^(\circ) \ and \ m\angle 8=75^(\circ)`