So firstly, we need to isolate the absolute value onto one side. To do this, we must first add both sides by 2:
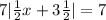
Next, divide both sides by 7:
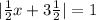
Now, we can split this equation to 2 equations:

Let's start with the first equation. Firstly, subtract both sides by 3 1/2:
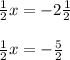
Lastly, multiply both sides by 2 and your first answer will be

Now, to the second equation. Firstly, subtract both sides by 3 1/2:
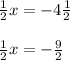
Lastly, multiply both sides by 2 and your second answer will be
