Question

There are 2 telephone companies in a city. Telephone Company A charges a flat fee of $27.50 each month plus $0.09 per minute for all long distance calls. Telephone Company B charges a flat fee of $26.80 each month plus $0.10 per minute for all long distance calls. For how many long distance minutes would the charges of both companies be equal?

Answer 1

From the given information we can see that,

Telephone company A charges a flat fee of $27.50 plus $0.09 per minute for all long distance calls.

Telephone company B charges a flat fee of $26.80 plus $0.10 per minute for all long distance calls.

Now the equation to represent the charges made by telephone company A is given by :

`C_1=27.50+0.09x`

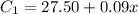
Where 'x' is the number of minutes long distance calls were made by using telephone company A.

The equation to represent charges made by telephone company B is given by:

`C_2=26.80+0.10x`

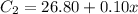
Where 'x' is the number of minutes long distance calls were made by using telephone company B.

As per our question we need to find the duration of long distance call so that charges for both the companies be equal, which implies

`C_1=C_2`

So,

`27.50+0.09x=26.80+0.10x`

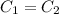
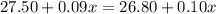
Solving for 'x', we get:

`27.50-26.80=(0.10-0.09)x`

`0.70=0.01x`

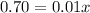
Therefore,

`x=(0.70)/(0.01) =70`

So, for 70 minutes of long distance call both the companies would charge the equal amount.