Answer: 17 m/s
Velocity and acceleration are vector quantities. Let leftwards be defines as negative and rightwards as positive direction.
It is given that canoe is drifting left with a velocity of
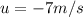
The canoe rider is moving towards right with a constant acceleration,
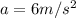
we need to find the velocity of canoe after 4 s.
we will use the equation of motion:
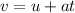
where, v is the final velocity, u is the initial velocity, a is the acceleration and t is the time.
Insert the values in the above equation:
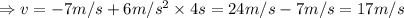
Hence, velocity of canoe after 4 s would be 17 m/s.