Question

Two mechanics worked on a car. the first mechanic worked for 5 hours, and the second mechanic worked for 15 hours. together they charged a total of $1575. what was the rate charged per hour by each mechanic if the sum of the two rates was $155 per hour?

Answer 1

Two mechanics worked on a car.

Now, mechanic 1 has spent 5 hours working on the car.

Mechanic 2 has spent 15 hours working on the car.

Lets say mechanic 1 charged 'x' dollars per hour and mechanic 2 charged 'y' dollars per hour.

So,

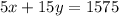`5x+15y=1575` that is our first equation ( 1 ):

And,

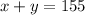`x+y=155` that is our second equation ( 2 ):

Using the two equations we can solve for 'x' and 'y', using our first equation we get:

`x+3y=315`

`x+y=155`

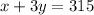
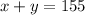
On solving for 'x' and 'y' we get:

`y=80`

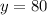
and putting the value of 'y' in the equation 2 we get:

`x=155-80=75`

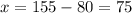
As mentioned earlier, 'x' represents the charge that mechanic 1 charged per hour and 'y' represents the charge that mechanic 2 charged per hour.

We have
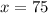`x=75` and
`y=80`.

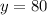So, the mechanic 1 charged $75 per hour and mechanic 2 charged $80 per hour.