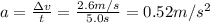Question

6. Using trigonometry, solve for the x and y components of the following: a. 17.0 m/s @ 30.0o c. 13.0 m/s2 @ 120o b. 19.0m@240o d. 22.0m/s@300o 7. Usingthecomponentsbelow,sketchthevectorwithlabeledcomponentsand calculate its magnitude and direction. a. Ax =34.0m,Ay =-34.0m b. Bx =0.00km,By =150.0km c. Cx = -8.00 m/s2, Cy = 6.00 m/s2 8. A girl holds a stick at an angle with one end on the ground and the other end 0.750 m above the ground. The Sun shines straight downward on the stick, and the stick makes a shadow on the ground that is 1.25 m long. What is the length of the stick and the angle it makes with the ground? 9. A boat travels on a heading of 40.0o north of east for a distance of 300 km. How far north and how far east of its starting point does the boat sail? 10.A weather station releases a weather balloon. The balloon’s buoyancy accelerates it upward at 15 m/s2. At the same time, a wind accelerates it horizontally to the right at 6.5 m/s2. What is the resulting acceleration? 11.Using the analytical method of vector addition, sketch and solve the following: a. 9.0m@55o +6.0m@125o b. 22.0 m/s @ 225o + 40.0 m/s @ 315o c. 17.0 m/s2 @ 330o - 11.0 m/s2 @ 270o 12.A car travels along a curved section of road. Initially the car has velocity 30.0 m/s @ 90.0o. After 5.00 s the car has a velocity of 30.0 m/s @ 95.0o. a. Calculate the change in the car's velocity. b. Calculate the car's average acceleration.

I have all of the answers already, but I need to show work. If you could pls show the work for me that would be such a help!! Thanks!

Answer 1

6a) Vector: 17.0 m/s @
`30.0^(\circ)`

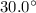
x-component:
`a_x = (17.0) cos 30.0^(\circ)=14.7 m/s`

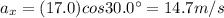
y-component:
`a_y = (17.0) sin 30.0^(\circ)=8.5 m/s`

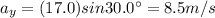
6b) Vector: 13.0 m/s^2 @
`120^(\circ)`

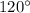
x-component:
`b_x = (13.0) cos 120.0^(\circ)=-6.5 m/s^2`

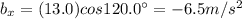
y-component:
`b_y = (13.0) sin 120.0^(\circ)=11.3 m/s^2`

6c) Vector: 19.0 m @
`240^(\circ)`

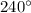
x-component:
`c_x = (19.0) cos 240.0^(\circ)=-9.5 m`

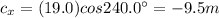
y-component:
`c_y = (19.0) sin 240.0^(\circ)=-16.4 m/s`

6d) Vector: 22.0 m/s @
`300^(\circ)`

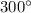
x-component:
`d_x = (22.0) cos 300.0^(\circ)=11 m/s`

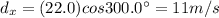
y-component:
`d_y = (22.0) sin 300.0^(\circ)=-19.0 m/s`

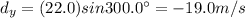
7a) Components: Ax =34.0m,Ay =-34.0m

Magnitude:
`|a|= √(A_x^2 +A_y^2)=√((34.0)^2+(-34.0)^2)=48.0 m`

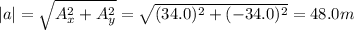
Direction:
`\theta=arctan((A_y)/(A_x))=arctan((-34.0)/(34.0))=arctan(-1)=-45^(\circ)`

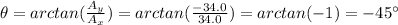
7b) Components: Bx =0.00km,By =150.0km

Magnitude:
`|b|= √(B_x^2 +B_y^2)=√((0)^2+(150.0)^2)=150.0 km`

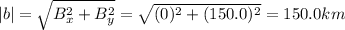
Direction:
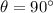`\theta=90^(\circ)` since it is in the y-direction (no component on x)

7c) Components: Cx = -8.00 m/s2, Cy = 6.00 m/s2

Magnitude:
`|c|= √(C_x^2 +C_y^2)=√((-8.0)^2+(6.0)^2)=10.0 m/s^2`

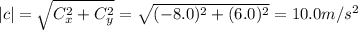
Direction:
`\theta=arctan((C_y)/(C_x))=arctan((6.0)/(-8.0))=arctan(-0.75)=-36.8^(\circ)`

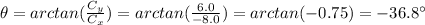
8) In this problem, 0.750 m corresponds to the vertical side and 1.25 m corresponds to the horizontal side of a right triangle. The length of the stick corresponds to the length of the hypothenuse of this triangle, that can be found using the Pytagorean's theorem:

`L=√((0.750 m)^2+(1.25 m)^2)=1.458 m`

The angle the stick makes with the ground is given by:

`\theta=arctan ((0.750 m)/(1.25 m))=arctan(0.6)=31.0^(\circ)`

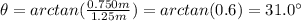
9) The displacement of the boat corresponds to a vector of length L=300 km and angle
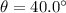`\theta=40.0^(\circ)` with respect to east. Therefore, the two components in the north and east directions are:

- north:
`L_y = L sin 40^(\circ)=(300 km)sin 40^(\circ)=192.8 km`

- east:
`L_x = L cos 40^(\circ)=(300 km) cos 40^(\circ) =229.8 km`

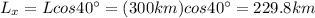
10) The two accelerations correspond to the two sides of a right triangle, therefore the resultant acceleration corresponds to the length of the hypothenuse of the triangle:

`a=√(a_x^2 +a_y^2 )=√((6.5)^2+(15)^2)=16.3 m/s^2`

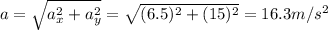
11a) 9.0m@55o +6.0m@125o

Let's resolve each vector in its components:

`v_(1x) = (9.0) cos 55^(\circ) = 5.2 m`

`v_(1y) = (9.0) sin 55^(\circ) = 7.4 m`

`v_(2x) = (6.0) cos 125^(\circ) = -3.4 m`

`v_(2y) = (6.0) sin 55^(\circ) = 4.9 m`

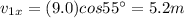
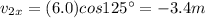
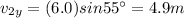
Now we sum the components in each direction:

`R_x = v_(1x)+v_(2x)=5.2-3.4 =1.8 m`

`R_y = v_(1y)+v_(2y)=7.4+4.9 =12.3 m`

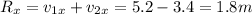
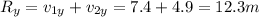
So the magnitude of the resultant vector is:

`R=√(R_x^2+R_y^2)=√((1.8)^2+(12.3)^2)=12.4 m`

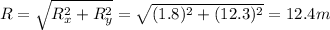
And the direction is:

`\theta=arctan((R_y)/(R_x))=arctan((12.3)/(1.8))=81.7^(\circ)`

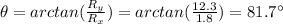
11b) 22.0 m/s @ 225o + 40.0 m/s @ 315o

Let's resolve each vector in its components:

`v_(1x) = (22.0) cos 225^(\circ) = -15.6 m/s`

`v_(1y) = (22.0) sin 225^(\circ) = -15.6 m/s`

`v_(2x) = (40.0) cos 315^(\circ) = 28.3 m/s`

`v_(2y) = (40.0) sin 315^(\circ) = -28.3 m/s`

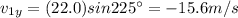
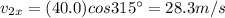
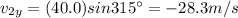
Now we sum the components in each direction:

`R_x = v_(1x)+v_(2x)=15.6+28.3 =43.9 m/s`

`R_y = v_(1y)+v_(2y)=-15.6-28.3 =-43.9 m/s`

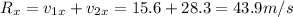
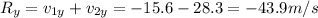
So the magnitude of the resultant vector is:

`R=√(R_x^2+R_y^2)=√((43.9)^2+(-43.9)^2)=62.1 m/s`

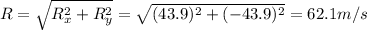
And the direction is:

`\theta=arctan((R_y)/(R_x))=arctan((-43.9)/(43.9))=315^(\circ)`

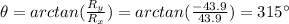
11c) 17.0 m/s2 @ 330o - 11.0 m/s2 @ 270o

Let's resolve each vector in its components:

`v_(1x) = (17.0) cos 330^(\circ) = 14.7 m/s`

`v_(1y) = (17.0) sin 330^(\circ) = -8.5 m/s`

`v_(2x) = (11.0) cos 270^(\circ) = 0 m/s`

`v_(2y) = (11.0) sin 270^(\circ) = -11 m/s`

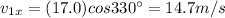
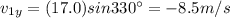
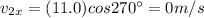
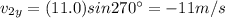
Now we calculate the difference between the components in each direction:

`R_x = v_(1x)+v_(2x)=14.7-0 =14.7 m/s`

`R_y = v_(1y)+v_(2y)=-8.5-(-11) =2.5 m/s`

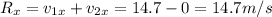
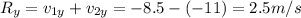
So the magnitude of the resultant vector is:

`R=√(R_x^2+R_y^2)=√((14.7)^2+(2.5)^2)=14.9 m/s`

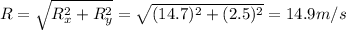
And the direction is:

`\theta=arctan((R_y)/(R_x))=arctan((2.5)/(14.7))=9.7^(\circ)`

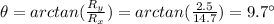
12a) The change in velocity is equal to the vector difference between the final velocity (vf) and the initial velocity (vi), so let's proceed as in the previous exercise:

`v_(1x) = (30.0) cos 90^(\circ) = 0 m/s`

`v_(1y) = (30.0) sin 330^(\circ) = 30 m/s`

`v_(2x) = (30.0) cos 95^(\circ) = -2.6 m/s`

`v_(2y) = (30.0) sin 95^(\circ) = 29.9 m/s`

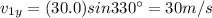
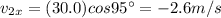
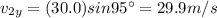
Difference:

`R_x = v_(2x)-v_(1x)=-2.6-0 =-2.6 m/s`

`R_y = v_(2y)-v_(2x)=29.9-(30) =-0.1 m/s`

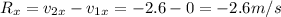
Magnitude of the resultant vector:

`R=√(R_x^2+R_y^2)=√((2.6)^2+(0.1)^2)=2.6 m/s`

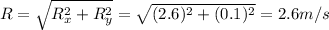
12b) Acceleration:
`a=(\Delta v)/(t)=(2.6 m/s)/(5.0 s)=0.52 m/s^2`