Question

10) Make a table of values for the rule x2 + x + 11 when x is an integer from 1 to 8. Make a conjecture about the type of number generated by the rule. Continue your table. What value of x generates a counterexample?

Answer 1

We have been given a rule
`x^(2)+x+11` and we are required to prepare a table of values using this rule and values of x from 1 to 8.

For x=1, we get:
`1^(2)+1+11=13`

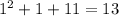
For x=2, we get:
`2^(2)+2+11=17`

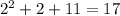
For x=3, we get:
`3^(2)+3+11=23`

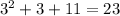
For x=4, we get:
`4^(2)+4+11=31`

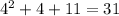
For x=5, we get:
`5^(2)+5+11=41`

For x=6, we get:
`6^(2)+6+11=53`

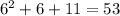
For x=7, we get:
`7^(2)+7+11=67`

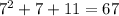
For x=8, we get:
`8^(2)+8+11=83`

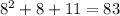
We can see that all these values are prime numbers. So, we can make a conjecture that the given rule produces prime numbers.

Now we need to find a counter example, that is, a value of x that produces a non-prime number, that is, a composite number.

Let us calculate the value of the given function at x=10. We get the value of the function as:

For x=10, we get:
`10^(2)+10+11=121`

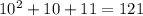
We know that 121 is a composite number as it is divisible by 11.

Therefore, x=10 generates a counter example.