Question

One way to remove nitrogen oxide from smokestack emissions is to react it with ammonia. 4NH3+6NO=5N2+6H2O Calculate a) the mass of water produced from 0.839 mol of ammonia. b) the mass of NO required to react with 3.402 mol of ammonia. c) the mass of ammonia required to produce 12.0 g of nitrogen gas. d) the mass of ammonia required to react with 115 g of NO.

Answer 1

(a) The mass of water produced will be, 22.653 grams.

(b) The mass of NO required will be, 153.09 grams.

(c) The mass of ammonia required will be, 5.8208 grams.

(d) The mass of ammonia required will be, 43.435 grams.

Explanation :

The balanced chemical reaction is,

`4NH_3+6NO\rightarrow 5N_2+6H_2O`

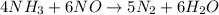
For (a) :

First have to calculate the moles of
`H_2O`.

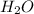From the balanced reaction, we conclude that

As, 4 moles of
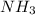`NH_3` react to give 6 moles of
`H_2O`

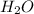
So, 0.839 moles of
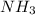`NH_3` react to give
`(6)/(4)* 0.839=1.2585moles of [tex]H_2O`

Now we have to calculate the mass of
`H_2O`.

`\text{Mass of }H_2O=\text{Moles of }H_2O* \text{Molar mass of }H_2O`

`\text{Mass of }H_2O=(1.2585mole)* (18g/mole)=22.653g`

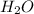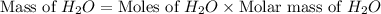
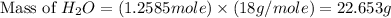
The mass of water produced will be, 22.653 grams.

For (b) :

Now we have to calculate the mass of NO required.

From the balanced reaction, we conclude that

As, 4 moles of
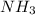`NH_3` react to give 6 moles of
`NO`

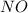
So, 3.402 moles of
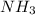`NH_3` react to give
`(6)/(4)* 3.402=5.103moles of [tex]NO`

Now we have to calculate the mass of
`NO`.

`\text{Mass of }NO=\text{Moles of }NO* \text{Molar mass of }NO`

`\text{Mass of }NO=(5.103mole)* (30g/mole)=153.09g`

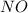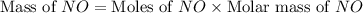
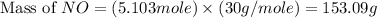
The mass of NO required will be, 153.09 grams.

For (c) :

First we have to calculate the moles of nitrogen gas.

`\text{Moles of }N_2=\frac{\text{Mass of }N_2}{\text{Molar mass of }N_2}=(12g)/(28g/mole)=0.428moles`

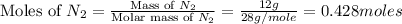
Now we have to calculate the moles of ammonia.

From the balanced reaction, we conclude that

As, 5 moles of
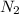`N_2` produced from 4 moles of
`NH_3`

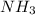
So, 0.428 moles of
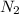`N_2` react to give
`(4)/(5)* 0.428=0.3424moles of [tex]NH_3`

Now we have to calculate the mass of
`NH_3`.

`\text{Mass of }NH_3=\text{Moles of }NH_3* \text{Molar mass of }NH_3`

`\text{Mass of }NH_3=(0.3424mole)* (17g/mole)=5.8208g`

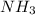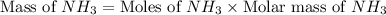
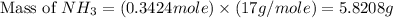
The mass of ammonia required will be, 5.8208 grams.

For (d) :

First we have to calculate the moles of NO.

`\text{Moles of }NO=\frac{\text{Mass of }NO}{\text{Molar mass of }NO}=(115g)/(g/mole)=3.833moles`

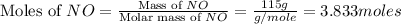
Now we have to calculate the moles of ammonia.

From the balanced reaction, we conclude that

As, 6 moles of
`NO` react with 4 moles of
`NH_3`

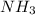
So, 3.833 moles of
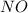`NO` react to give
`(4)/(6)* 3.833=2.555moles of [tex]NH_3`

Now we have to calculate the mass of
`NH_3`.

`\text{Mass of }NH_3=\text{Moles of }NH_3* \text{Molar mass of }NH_3`

`\text{Mass of }NH_3=(2.555mole)* (17g/mole)=43.435g`

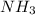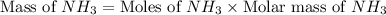
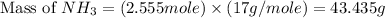
The mass of ammonia required will be, 43.435 grams.

Answer 2

a) 22.7 g H₂O; b) 153.1 g NO; c) 5.84 g NH₃; d) 43.5 g NH₃

a) Mass of water

= 0.839 mol NH₃ × (6 mol water/4 mol NH₃) × (18.02 g H₂O/1 mol H₂O)

= 22.7 g H₂O

b) Mass of NO

= 3.402 mol NH₃ × (6 mol NO/4mol NH₃) × (30.01 g NO/1 mol NO) = 153.1 g NO

c) Mass of NH₃

= 12.0 g N₂ × (1 mol N₂/28.01 g N₂) × (4 mol NH₃/5 mol N₂)

× (17.03 g NH₃/1 mol NH₃) = 5.84 g NH₃

d) Mass of NH₃

= 115 g NO × (1 mol NO/30.01 g NO) × (4 mol NH₃/6 mol NO)

× (17.03 g NH₃/1 mol NH₃) = 43.5 g NH₃