Question

On a certain​ river, a paddleboat travels 12 miles upstream ​(against the​ current) in the same amount of time it travels 20 miles downstream​ (with the​ current). If the current of the river is 2 miles per ​hour, determine the speed of the boat in still water.

Answer 1

We will take velocity of the boat Vb and velocity of the river Vr=2 mph

Distance D1=12 miles and distance D2=20 miles and t is the time.

First equation is (Vb-Vr) * t = D1 and the second is (Vb+Vr) * t = D2

When we replace data we have we get

(Vb-2) *t = 12 and (Vb+2) * t = 20

From the first equation t= 12/(Vb-2)

From the second equation t=20/(Vb+2)

If the left sides of equations are equal then the right sides are equal too,

and we get 12/(Vb-2)=20/(Vb+2) then we multiply crosswise and get

12*(Vb+2)=20*(Vb-2) => 12Vb+24=20Vb-40 => 20Vb-12Vb=40+24 =>

8Vb=64 => Vb=64/8=8mph Velocity ( or speed) of the boat is Vb= 8mph

Good luck!!!

Answer 2

Given :

a paddle boat travels upstream = 12 miles

a paddle boat travels downstream = 20 miles

speed of the current = 2 miles per ​hour

Let the speed of the boat =x

Let the time taken = t

We know the distance for upstream D= (boat speed - current speed) * time

the distance for downstream D= (boat speed + current speed) * time

Plug in all the values and variables in the distance

For upstream 12 = (x-2)t, then
`t = (12)/(x-2)`

For downstream 20 = (x+2)t then
`t = (20)/(x+2)`

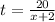
we got two equations for t, equate it and solve for x

`(12)/(x-2) = (20)/(x+2)`

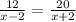
Cross multiply it

12(x+2) = 20(x-2)

12x + 24 = 20x - 40 (subtract 12x and add 40 on both sides)

64 = 8x

x= 8

the speed of the boat in still water = 8 miles per hour