Answer:
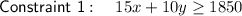
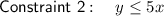
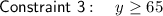
Explanation:
Inequality signs:
- < Less than.
- ≤ Less than or equal to.
- > More than.
- ≥ More than or equal to.
Given variables:
- x = Number of lawns mowed.
- y = Number of dogs walked.
Constraint 1
Given information:
- $15 = Charge for mowing a lawn.
- $10 = Charge for walking a dog.
- $1850 = Minimum amount needed for the trip.
Therefore, the amount earned from mowing the lawns and walking dogs should be more than or equal to $1850:
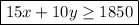
Constraint 2
Given information:
- The number of dog walks that Sarah has scheduled is no more than 5 times the number of lawns Jacob has scheduled to mow:
Therefore, Sarah will walk less than or equal to 5 times the number of lawns mowed:

Constraint 3
Given information:
- Sarah will walk at least 65 dogs.
Therefore, Sarah will walk more than or equal to 65 dogs:
