Answer:
Option B -
 and
and
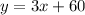
Explanation:
Given : The Thrill amusement park charges an entry fee of $40 and an additional $5 per ride, x. The Splash water park charges an entry fee of $60 and an additional $3 per ride, x.
To find : Which system of equations could be used to determine the solution where the cost per ride of the two amusement parks, y, is the same?
Solution :
Let x be the number of rides and
y be the cost per ride.
According to question,
The Thrill amusement park charges an entry fee of $40 and an additional $5 per ride.
The equation form is
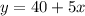
The Splash water park charges an entry fee of $60 and an additional $3 per ride.
The equation form is

Therefore, The required system of equations form are
 and
and
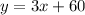
So,Option B is correct.