1. You have that the length of the yard is 10 feet more than 3 times the width. Then, you can write the following expression:
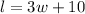
Where
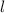 is the length and
is the length and
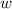 is the width.
is the width.
2. She needs 60 feet of fencing, which is the perimeter.
3. The formula of the perimeter of a rectangle is:
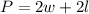
4. Therefore, you can substitute the first expression of the lenght into the formula of the perimeter and solve for the width:

5. Now you can calculate the length:

The answer is: The length of the yard is 25 feet.