This is likely what Jeremy did
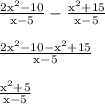
The error happens in line 2
This is what his steps should be
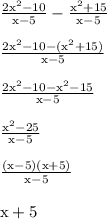
On the 2nd step, we subtract all of (x^2+15) and not just the x^2 part. The negative distributes to each term in step 3. Then we combine like terms, factor and cancel out the (x-5) terms.
Therefore,
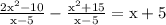 is an identity as long as
is an identity as long as
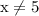 to avoid a division by zero error.
to avoid a division by zero error.