Question

An earthworm of length 15cm is crawling along at 2cm/s. An ant overtakes the worm in 5 seconds.How fast is the ant walking?

Answer 1

Assume we have a number line, where the tail of the worm is at x=0. This means that the head of the worm is at x=15.

Also, we know that the coordinate of the head of the worm follows this equation:

`x_H(t) = 15+2t`

Where
`t` is the time in seconds. In fact, we know that the worm gains 2 centimeters per second.

Now, assume that the ant also starts at x=0, and walks with a certain rate of
`v_A` centimeters per second. This means that the equation for the position of the ant is

`x_A(t) = v_At`

Now, we know that after 5 seconds the ant is in the same position as the head of the worm, which means

`x_A(5) = x_H(5)`

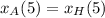
We know the equation for both expressions, so let's subtitute them in:

`5v_A = 15+2\cdot 5 \iff 5v_A = 15+10 \iff 5v_A = 25 \iff v_A = 5`

So, the ant walks at a rate of 5cm per second.