If AM=BM, then point M is a middle point of side AB.
1. Consider triangle AML. You know that AM=ML, then this triangle is isosceles and AL is its base. The angles adjacent to the base of isosceles triangle are conruent, this means that

2. Consider lines ML and AC. The angle bisector AL is transversal. Since alternate interior angles
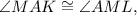 you have that lines ML and AC are parallel. This means that ML is a middle line of triangle and 2ML=AC. Also you know that AC=2AL. This gives you that ML=AL. Now ML=AL and ML=AM gives you that triangle AML is equilateral.
you have that lines ML and AC are parallel. This means that ML is a middle line of triangle and 2ML=AC. Also you know that AC=2AL. This gives you that ML=AL. Now ML=AL and ML=AM gives you that triangle AML is equilateral.
3. In equilateral triangle AML all angles are congruent and have measures 60°. Thus, m∠AML=m∠MLA=m∠LAM=60°.
4. AL is angle bisector, then m∠MAL=m∠LAC=60° and m∠BAC=m∠MAL+m∠LAC=120°.
5. Consider ΔBML, it is isosceles, because BM=ML and m∠BML=180°-m∠AML=180°-60°=120°. Then,
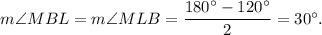
6. Consider triangle ABC. In this triangle m∠A=120°, m∠B=30°, then
m∠C=180°-m∠A-m∠B=180°-120°-30°=30°.
Answer: m∠A=120°, m∠B=m∠C=30°.