Question

3. For her chemistry experiment, Marisol needs 2 liters of a 50% alcohol solution. The lab has two containers, one with 40% alcohol solution, and the other with 80% alcohol solution.

(a) Write a system of linear equations that you can use to determine how many liters of each type of alcohol solution Marisol should combine to get 2 liters of a 50% alcohol solution. Be sure to define your variables.
(b) Solve the system and determine how many liters of each type of alcohol solution Marisol should combine. Show all your work.

Answer 1

Hello,

Please, see the attacheed files.

Thanks.

Answer 2

Let x l be the amount of 40% alcohol solution and y l be the amount of 80% alcohol solution.

1. Marisol needs 2 liters of a 50% alcohol solution. Then

x+y=2.

2. In x l of 40% alcohol solution is 0.4x l of alcohol, in y l of 80% alcohol solution is 0.8y l of alcohol and in 2 l of 50% alcohol solution is 0.5·2=1 l of alcohol. Then

0.4x+0.8y=1.

2. Solve the system of equations:

`\left\{\begin{array}{l}x+y=2\\0.4x+0.8y=1\end{array}\right.`

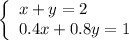
From the first equation

`x=2-y.`

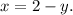
Substitute it into the second equation:

`0.4(2-y)+0.8y=1,\\ \\0.8-0.4y+0.8y=1,\\ \\0.4y=1-0.8=0.2,\\ \\y=(0.2)/(0.4)=0.5\ l.`

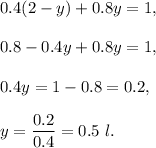
Then

`x=2-y=2-0.5=1.5\ l`

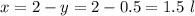
Answer: Marisol should combine 1.5 l 0f 40% alcohol solution with 0.5 l of 80% alcphol solution.