First we need to know what slope-intercept form is. Slope-intercept form is y = mx + b, where m is the slope, and b is the y coordinate of the y-intercept.
To find the equation for a line in slope-intercept form using a line on a graph, you would first find the slope of the line using two points from the graph that the line is intersecting. This is for your "m" in y = mx + b.
Then you would look at the graph to see exactly where the line intersects the y-axis (vertical axis) for your "b" in y = mx + b.
Let's find the slope of the line first. To find the slope of the line we will use two points from the graph that the line intersects. Let's use (0, 8) and (10, 0) because these are points that the line crosses "perfectly".
The slope can be found using the formula
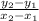 , where y_2 and y_1 are the y coordinates in the points that we are using (x, y) ⇒ (0, 8) and (10, 0), and x_2 and x_1 are the x coordinates in the points, (0, 8) and (10,0).
, where y_2 and y_1 are the y coordinates in the points that we are using (x, y) ⇒ (0, 8) and (10, 0), and x_2 and x_1 are the x coordinates in the points, (0, 8) and (10,0).
You could really subtract the y-coordinates in any order, but then your x-coordinates would have to be subtracted the same order. So say you subtract y_1 - y_2, then you would have to subtract x_1 - x_2, not x_2 - x_1. We will be subtracting y_2 - y_1.
Substitute the x and y coordinates into the formula. Your formula should now look like this:
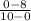 . Subtract the coordinates and solve for the slope.
. Subtract the coordinates and solve for the slope.
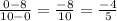 , so your slope is -4/5. You've solved for "m" in the slope-intercept form, now we will solve for "b" (y-intercept) in y = mx + b.
, so your slope is -4/5. You've solved for "m" in the slope-intercept form, now we will solve for "b" (y-intercept) in y = mx + b.
This part is much easier when doing so on a graph; just look at the y-axis (vertical) and see exactly where the line is intersecting it at. The line intersects the y-axis exactly at (0, 8), so b will be "8" because it is the y-coordinate of the y-intercept.
Substitute in everything we have found into the formula y = mx + b. We'll substitute -4/5 for x and 8 for b, so now we have: y = -4/5x + 8 as your answer.