Question

chuck sold 117 tickets for a play. Tickets cost $5, but they also sold discounted tickets at $2 for children. if profits were $483, how many of each kind of ticket were sold

Answer 1

To solve this problem, we can write two equations, one showing the total number of tickets sold and the other showing the total profit. a is the number of adult tickets sold, and c is the number of child tickets.

`a + c = 117`
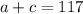
This shows the total number of tickets sold.
For the other equation (showing the profits), we can multiply the price of each ticket by the number sold, and add these together to find the profit:

`5a + 2c = 483`
To solve the problem, we can go back to the first equation and subtract c from both sides in order to write it in terms of a.

`a = 117 - c`
We can now enter this equation in the place of a in the second equation, and solve for c.

`5(117 - c) + 2c = 483 \\ 585 - 5c + 2c = 483 \\ - 3c = - 102 \\ c = 34`
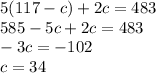
You now know that 34 children's tickets were sold. Using this information, you can go back to the earlier equation and find the number of adult tickets.

`a = 117 - c \\ a = 117 - 34 \\ a = 83`
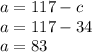
There were 83 regular tickets sold, and 34 children's tickets sold.

Answer 2

just use the given info to set up 2 equations and go from there

hope that helps