Question

A space probe is built with a mass of 1700 pound-mass [lbm] before launch on Earth. The probe is powered by four ion thrusters, each capable of generating 225 millinewtons [mN] of thrust. Using Newton’s second law, the acceleration (a) of the craft is equal to the force (F) divided by the mass (m): a = F/m The velocity (v) of an object increases as an object accelerates. If the object starts at rest, the final velocity is given by the acceleration multiplied by the length of time the acceleration is applied to the object (t): v = at = (Ft)/m Using this equation, how many weeks will the thrusters have to operate for the probe, initially at rest, to reach a velocity of 420 miles per minute [mi/min]? You may assume the initial velocity of the probe is zero miles per minute [0 mi/min]

Answer 1

The 64 weeks

Step-by-step explanation:

Thinking process:

First we gather the data:

1700lbm = 771.107 kg

225 milliNewtons = 0.225 N

Final velocity = 420 mil/min = 11 265.4 m/s

Let the initial velocity, u₀ = 0 m/s

Final velocity = v m/s

Acceleration is given by the formula,
`a = (F)/(m) \\ =(0.225)/(771.107) \\ = 0.0002918 m/s^(2)`

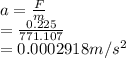
However, we know that the final velocity, v is given by
`v = u + at`

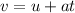
where u = 0

a = 0.0002918

t = ?

v = 11 265.4 m/s

substituting:

11 265.4 = 0 + (0.0002918) (t)

dividing both sides gives, t = 38 606 579 s

1 day = 86 400 s

t = 446.83 days

= 63.8 weeks

= 64 weeks