Question

If point k is the midpoint of segment HJ, HK=(3x-10) units, and HJ=(4x+19) units, then,

x=__
HK=__
HJ=__
KJ=__

Answer 1

x=

Explanation:

Given the midpoint formula: (
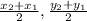`(x_2+x_1)/(2),(y_2+y_1)/(2)`),the Segment Addition Postulate, and the line attached, find x, HK, HJ, KJ

1st step is in the picture.

doing the first step gives us
`x + 9`

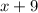
Since k is the midpoint, both sides of the midpoint are the same length

so we can use the equation
`3x - 10 = x+9`

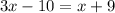
subtract x from both sides:
`3x-10-x=x+9-x`

`2x-10=9`

`2x-10+10=9+10`

`2x=19`

`2x/2=19/2`

`x=9.5`

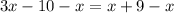
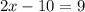
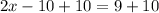
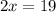
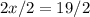
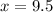
Now that we know x, we can substitute to find HK, HJ, and KJ

`HK = 3(9.5)-10`

`HJ = 4(9.5)+19`

`KJ = x +9`

`HK = 28.5 -10\\HJ = 38+19\\\\KJ = 9.5 + 9\\HK = 18.5\\HJ=57\\KJ = 18.5\\`

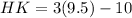
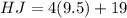
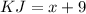
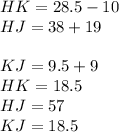
Our HK and KJ answer is correct because they are the same, and the midpoint of HK and KJ is point K.