Question

In a right triangle ABC, CD is an altitude, such that AD=BC. Find AC, if AB=3 cm, and CD= root 2 cm.

PLZ ANSWER!

Answer 1

Given CD is an altitude such that AD=BC , AB=3 cm and CD= √2 cm.

Let AD=x, Since given AB=3

AD+DB=3

x+DB = 3

DB = 3-x

Since ΔBCD is rght angle triangle, let's apply Pythagoras theorem

`BC^(2) = DB^(2) +CD^(2)`

`BC^(2) = (3-x)^(2) +(√(2) )^(2)`

`BC^(2) =(3-x)^(2) +2`

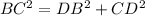
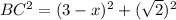
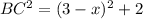
Since given AD=BC,let us plugin BC=x in above step.

`x^(2) =(3-x)^(2) +2`

`x^(2) =9-6x+x^(2) +2`

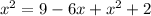
6x=11

x=
`(11)/(6)`

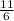
Now we know AD=x=
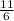`(11)/(6)` and given CD=√2.

Let us apply Pythagoras theorem for ΔACD

`AC^(2) =AD^(2) +DC^(2)`

`AC^(2) = ((11)/(6) )^(2) +(√(2) )^(2)`

`AC^(2) =(193)/(36)`

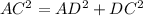
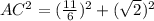
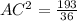
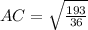`AC=\sqrt{(193)/(36) }` = 2.315cm