Question

Find the y intercepts of 3x^2+24x-51. quadratic formula

Answer 1

• Quadratic Formula:
  `x=(-b\pm √(b^2-4ac))/(2a)` , with a = x^2 coefficient, b = x coefficient, and c = constant.

Firstly, starting with the y-intercept. To find the y-intercept, set the x variable to zero and solve as such:

`y=3*0^2+24*0-51\\y=0+0-51\\y=-51`

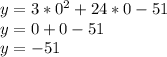
Your y-intercept is (0,-51).

Next, using our equation plug the appropriate values into the quadratic formula:

`x=(-24\pm √(24^2-4*3*(-54)))/(2*3)`

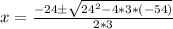
Next, solve the multiplications and exponent:

`x=(-24\pm √(576-(-648)))/(6)\\\\x=(-24\pm √(576+648))/(6)`

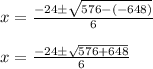
Next, solve the addition:

`x=(-24\pm √(1224))/(6)`

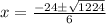
Now, simplify the radical using the product rule of radicals as such:

• Product Rule of Radicals: √ab = √a × √b

√1224 = √12 × √102 = √2 × √6 × √6 × √17 = 6 × √2 × √17 = 6√34

`x=(-24\pm 6√(34))/(6)`

Next, divide:

`x=-4\pm √(34)`

The exact values of your x-intercepts are (-4 + √34, 0) and (-4 - √34, 0).

Now to find the approximate values, solve this twice: once with the + symbol and once with the - symbol:

`x=-4+ √(34),-4- √(34)\\x\approx 1.83, -9.83`

The approximate values of your x-intercepts (rounded to the hundredths) are (1.83,0) and (-9.83,0).