Question

the base of a triangle exceeds the height by 5 yards. if the area is 187 square yards, find the length of the base and height of the triangle?

Answer 1

We know that the base of the triangle is 5 yards more than the height of the triangle

Let base of the triangle be 'b' and height of the triangle be 'h'

⇒ b = h + 5

Also, we have been given that the area of the triangle is 187 square yards

We have to determine the length of the base and height of the triangle.

`Area = (1)/(2) * b * h`

⇒
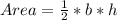
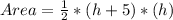`Area = (1)/(2) * (h+5) * (h)` = 187

⇒ \frac{1}{2} * (h+5) * (h)[/tex] = 187

⇒
`(h^(2)+5h)/(2) = 187`

⇒
`h^(2)+5h = 187 * 2`

⇒
`h^(2)+5h - 374 = 0`

⇒
`h^(2)+22h -17h - 374 = 0`

⇒
`h (h+22) - 17 (h+22) = 0`

⇒
`(h-17) (h+22) = 0`

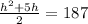
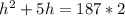
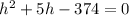
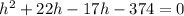
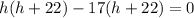
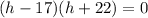
⇒ h = 17 or h = -22

Since height can't be negative, so h = 17 yards

⇒ b = h + 5 = 17+5 = 22 yards

Hence, height of the triangle is 17 yards and the base is 22 yards.