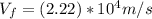Question

A uniform electric field exists in the region between two oppositely charged plane parallel plates. A proton is released from rest at the surface of the positively charged plate and strikes the surface of the opposite plate, 1.70 cm distant from the first, in a time interval of 1.48×10−6 s .

Find the magnitude of the electric field.


Find the speed of the proton when it strikes the negatively charged plate.

Answer 1

The magnitude of the electric field can be calculated using the equation

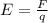`E = (F)/(q)`, where F is the Force acting on the proton and q is the charge of the proton.

We know that the charge of the proton is
`q = 1.6 x 10^(-19)  C`

We have to calculate the Force first.

We know that F = ma from Newton's 2nd law, where m is the mass of the proton and a is the acceleration.

We know that the mass of the proton
`m = (1.67) X 10^(-27)  kg`

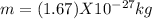
So it turns out that we have to calculate acceleration before anything else.

In order to calculate the acceleration, we make use of the following data from the question:

Initial Velocity of the proton
`V_(i)  = 0`

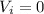
Distance traveled
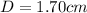`D = 1.70 cm` = 0.017 m

Time taken for the travel between the plates
`t = (1.48) X 10^(-6)  s`

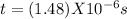
Acceleration a = ?

Using the equation,
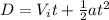`D = V_(i)t + (1)/(2) at^(2)`, we get

Knowing that initial velocity is 0, the equation reduces to
`D = (1)/(2)at^(2)`

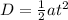
Rearranging the equation so as to make a the subject of the formula, we have

`a = (2D)/(t^(2) )`

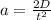
Plugging in the numbers and simplifying gives us a = 1.5 x
`10^(10)   m/s^(2)`

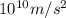
We can now calculate the Force using F = ma

Plugging in the known values, we get F = 2.5 x
`10^(-17)  N`

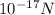
Using this, we can calculate E through the equation
`E = (F)/(q)`

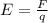
Plugging the numbers and simplifying gets us E = 156.25 N/C

Thus, the magnitude of the electric field between the plates of the capacitor is 156.25 N/C

B) To calculate the Final Velocity of the proton, we can make use of the equation

`V_(f)  = V_(i)  + at`

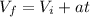
Plugging the numbers in and simplifying gets us
`V_(f)  = (2.22)  *  10^(4)  m/s`

Answer 2

1) Magnitude of the electric field

The distance traveled by the proton is equal to the distance between the two plates:

d = 1.70 cm = 0.017 m

And the proton takes
`t=1.48 \cdot 10^(-6)s` to cover this distance. From these data, we can find the acceleration experienced by the proton

`a=(2d)/(t^2)=(2(0.017 m))/((1.48 \cdot 10^(-6) s)^2)=1.55 \cdot 10^(10) m/s^2`

But we know that the electric force F exerted on the proton is equal to the proton mass (m) times the acceleration (a):

`F=ma=(1.67 \cdot 10^(-27) kg)(1.55 \cdot 10^(10) m/s^2)=2.59 \cdot 10^(-17) N`

and since the electric force is equal to the electric field strength, E, times the proton charge, q: F=qE, we can find E:

`E=(F)/(q)=(2.59 \cdot 10^(-17) N)/(1.6 \cdot 10^(-19) C)=161.88 N/C`

2) Speed of the proton as it strikes the negative plate

Since the proton starts from rest, its speed at time t is given by:

`v(t) = at`

substituting the values of acceleration and time that we found in the previous part of the problem, we can calculate the speed of the proton:

`v=at=(1.55 \cdot 10^(10) m/s^2)(1.48 \cdot 10^(-6) s)=22940 m/s`