Question

To practice tactics box 5.2 working with objects in contact. a 1200-kg car pushes a 2100-kg truck that has a dead battery to the right. when the driver steps on the accelerator, the drive wheels of the car push against the ground with a force of 4500 n . what is the magnitude of the force the car applies to the truck

Answer 1

Answer : F = 2856 N

Explanation :

It is given that,

Mass of car,
`m_c=1200\ kg`

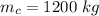
Mass of truck,
`m_t=2100\ kg`

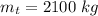
Force that pushed against the ground,
`F=4500\ N`

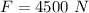
When the driver steps on the accelerator, the total force F acts on the total mass i.e the mass of the car and that of truck m = 1200 kg +21000 kg = 3300 kg.

From Newton's second law :

F = ma

`a=(F)/(m)`

`a=(4500\ N)/(3300\ kg)`

`a=1.36\ m/s^2`

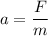
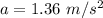
a is the acceleration when the wheels of the car push against the ground.

To find the magnitude of the force the car applies to the truck, we have to use again Newton's second law :

`F=m_t\ a`

`F=2100\ kg* 1.36\ m/s^2`

`F=2856\ N`

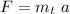
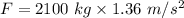
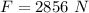
So, the force the car applies to the truck is 2856 N.

Hence, this is the required solution.

Answer 2

Mass of the car = 1200 kg

Mass of the truck = 2100 kg

Total mass of car and truck = 2100 + 1200 = 3300 kg

Since, the car pushes the truck. Hence, they will move together and will have same acceleration.

Let the acceleration be a.

According to Newton's second law:

F(net) = ma

F = 4500 N

4500 = 3300 × a

`a = (4500)/(3300)`

a = 1.36 m/s^2

Let the force applied by the car on truck be F.

F = F(net) on the truck

F = ma

F = 2100 × 1.36

F = 2856 N

Hence, the force applied by the car on the truck is 2856 N