Given
balloon rises straight up at a rate of 120 ft per min.
balloon is tracked from a rangefinder on the ground at point p, which is 400 ft from the release point q of the balloon.
d = the distance from the balloon to the rangefinder and t= the time in mins
Express d as a function of t.
To proof = With the help the diagram as shown in below .
balloon rises straight up at a rate of 120 ft per min.
thus RQ = 120t
rangefinder on the ground at point p, which is 400 ft from the release point q of the balloon.
thus PQ = 400 ft
Let PR =d
by using the pythagoras theorem
we have
RQ² + PQ² = PR²
now putting the value
we have
(120t)² + 400² = d²
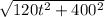 = d
= d
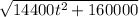 = d
= d
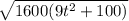 = d
= d
 ft
ft
hence d is express in the term of t
Hence proved