Let the key is free falling, therefore from equation of motion
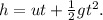 .
.
Take initial velocity, u=0, so
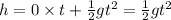 .
.
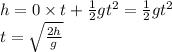
As velocity moves with constant velocity of 3.5 m/s, therefore we can use formula
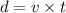
From above substituting t,
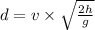 .
.
Now substituting all the given values and g = 9.8 m/s^2, we get
 .
.
Thus, the distance the boat was from the point of impact when the key was released is 10.60 m.