Question

He georgetown, south carolina, traffic division reported 40% of high-speed chases involving automobiles result in a minor or major accident. during a month in which 50 high-speed chases occur, what is the probability that 25 or more will result in a minor or major accident?

Answer 1

Answer: The probability that 25 or more out of 50 high speed chases result in minor or major accidents is 0.097807364 or 9.781%.

The rate of accidents at 0.40 is a constant rate, and hence we can use the binomial distribution to calculate the probability.

The formula for computing the probability with the binomial distribution is:

`P(X=x) = _(n)C_(x)*p^(x)*q^(n-x)`

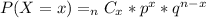
where

N is number of trials = 50

p is probability of of a hit in a single trial. In this case, p = 0.40

q is probability of of a miss in a single trial. Now
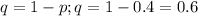`q = 1 - p; q = 1 - 0.4 = 0.6` for this question

x will take on the whole numbers from 25 and continue upto 50

The questions asks us to compute the probability that 25 or more chases will result in an accident.

We express this as P( X≥ 25) mathematically.

We can also express P( X≥ 25) as P (x=25) + P(x=26) + ................ + P(50) i.e the sum of all the individual probabilities when x assumes each of the values from 25 upto 50.

That's why x will take on each of the whole numbers from 25 to 50.

We can compute P( X=25) by substituting the values in the formula above.

`P(X=25) = _(50)C_(25)*0.4^(25)*0.6^(50-25)`

`P(X=25) = (n!)/(x!*(n-x)!)*0.4^(25)*0.6^(50-25)`

`P(X=25) = (50!)/(25!*(50-25)!)*0.4^(25)*0.6^(50-25)`

`P(x=25) = 0.040463604`

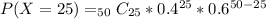
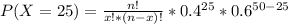
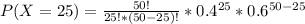
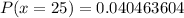
Similarly we need to compute the probabilities for x =26, 27 and so on until x =50. The sum total of all these probabilities the answer.

The workings have been made in excel and are attached to this answer as a picture.