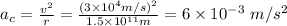In 1 year, 365 days, each day 24 hours, each hour 60 minutes and each minute 60 seconds.
OR
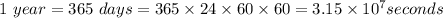 .
.
As the radius of the earth's very nearly circular orbit around the sun is 1.5 x 10^11 m.
Therefore, the magnitude of the earth's velocity
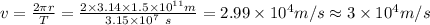 .
.
The magnitude of the earth's angular velocity is
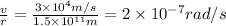 .
.
The magnitude of the earth's centripetal acceleration is