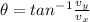Question

The acceleration of a particle moving only on a horizontal xy plane is given by modifyingabove a with right-arrow equals 5t modifyingabove i with caret plus 6t modifyingabove j with caret, where modifyingabove a with right-arrow is in meters per second-squared and t is in seconds. at t = 0, the position vector modifyingabove r with right-arrow equals left-parenthesis 29.0mright-parenthesis modifyingabove i with caret plus left-parenthesis 45.0mright-parenthesis modifyingabove j with caret locates the paticle, which then has the velocity vector modifyingabove v with right-arrow equals left-parenthesis 5.50 m/s right-parenthesis modifyingabove i with caret plus left-parenthesis 3.10 m/s right-parenthesis modifyingabove j with caret. at t = 5.20 s, what are (a) its position vector in unit-vector notation and (b) the angle between its direction of travel and the positive direction of the x axis?

Answer 1

acceleration of the object is given as

`a = 5t\hat i + 6 t\hat j`

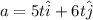
at t = 0 its position vector is

`r_i = 29 \hat i 45 \hat j`

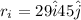
and its initial velocity is given as

`v_i = 5.5\hat i + 3.10\hat j`

now in order to find the velocity we will integrate the acceleration

`a = (dv)/(dt)`

`v - v_i = \int a dt`

`v - (5.5\hat i + 3.10\hat j) = \int 5t \hat i + 6t \hat j dt`

`v = (5.5 + 2.5 t^2)\hat i + (3.10 + 3t^2)\hat j`

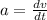
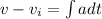
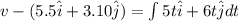
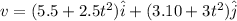
at t = 5.20

`v = 73.1 \hat i + 84.22\hat j`

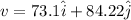
now position vector is integration of velocity

`v = (dr)/(dt)`

`r - (29 \hat i +  45 \hat j) = \int v dt`

`r = (29 \hat i + 45 \hat j) + \int ((5.5 + 2.5 t^2)\hat i + (3.10 + 3t^2)\hat j)dt`

`r = (29 + 5.5t + 0.833 t^3)\hat i + (45 + 3.10t + t^3)\hat j`

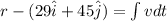
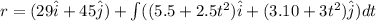
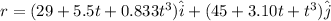
at t = 5.20 s

`r = 174.7 \hat i + 201.7\hat j`

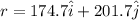
Part b)

now in order to find the direction

`\theta = tan^(-1)(v_y)/(v_x)`

`\theta = tan^(-1)(84.22)/(73.1) = 49 degree`