Question

A ball is dropped from the top of a building. the balls fall 3 times farther during its last second of freefall than it did during its third second of freefall. the ball fell 4.9 meters during its first second, how tall is the building and how much time is the ball in the air?

Answer 1

Height of building = 313.6 meter.

The ball is in air for 8 seconds.

Step-by-step explanation:

We have equation of motion ,
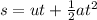`s= ut+(1)/(2) at^2`, s is the displacement, u is the initial velocity, a is the acceleration and t is the time.

We have u = 0 m/s and s = 4.9 when t = 1 seconds.

`4.9= 0*1+(1)/(2) a*1^2\\\\ a=9.8m/s^2`

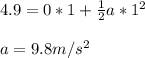
Distance fallen in third second = Distance fallen till third seconds - Distance fallen till two seconds

`=0*3+(1)/(2) *9.8*3^2-(0*2+(1)/(2) *9.8*2^2)\\\\=(1)/(2) *9.8*(3^2-2^2)=24.5 m`

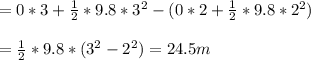
Let the time to reach ground be k seconds.

Distance fallen in
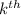`k^(th)` second = Distance fallen till k seconds - Distance fallen till (k-1) seconds =

`0*k+(1)/(2) *9.8*k^2-(0*(k-1)+(1)/(2) *9.8*(k-1)^2)\\\\=4.9*(k^2-(k-1)^2)\\\\=4.9*(k^2-k^2+2k-1)\\\\=4.9(2k-1)`

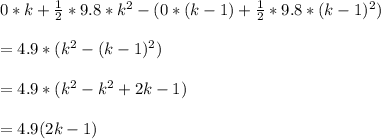
We have Distance fallen in
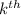`k^(th)` second = 3*Distance fallen in third second

= 24.5*3 = 73.5 meter.

So 4.9(2k-1) = 73.5

k = 8 seconds.

So distance fallen in eighth second = 3*Distance fallen in third second

Height of building = Distance fallen till 8 seconds

=
`0*8+(1)/(2) *9.8*8^2=313.6 meter.`

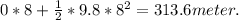
The ball is in air for 8 seconds.